---

In a previous post I discussed the use of Univariate Linear Regression and the Cost Function. This post will be about how we use Gradient Descent to find the best $\theta$ values for our Hypothesis Function.

---

Gradient Descent for Univariate Linear Regression

All of our logic for gradient descent is contained in the following:

$ \theta_j := \theta_j - \alpha \frac {\partial} {\partial\theta_j} J(\theta_0,\theta_1) $

We can break this down into something more understandable.

Key points

The difference between $:=$ and $=$ is that the former overwrites whatever is to the left of it whereas the latter is simply a truth assertion.

$\theta_j$ is simply a place holder for whatever $\theta$ we are reassigning. Either 1 or 2 in our case.

$\frac {\partial} {\partial\theta_j}$ is saying we will derive with respect to the $\theta$ we are working with. Again, 1 or 2 in our case.

$\alpha$ is the interval that we are adjusting our Descent too. This is called the learning rate. We use a fixed value here. This is very important because if the value is too large we will never converge on $\theta_0$ and $\theta_1$.

Derivation

First we will derive the cost function with respect to $\theta_0$.

$\frac {\partial} {\partial\theta_0} J(\theta_0,\theta_1)$ is equivalent to $\frac {\partial} {\partial\theta_0} \frac {1} {2m} \sum_{i=0}^n ( { h _\theta ( x^{(i)} ) } - y^{(i)} )^2$. We can also replace $h _\theta ( x^{(i)} )$ because $h_\theta(x) = \theta_0 + \theta_1x$ for univariate linear regression. We are left with $\frac {\partial} {\partial\theta_0} \frac {1} {2m} \sum_{i=0}^n ( \theta_0 + \theta_1x - y^{(i)} )^2$

The derivation from this point is trivial and we are left with:

$ \theta_0 := \theta_0 - \alpha \frac {\partial} {\partial\theta_0} \frac {1} {m} \sum_{i=0}^n ( \theta_0 + \theta_1 ( x^{(i)} ) - y^{(i)} )$

and

$ \theta_1 := \theta_1 - \alpha \frac {\partial} {\partial\theta_1} \frac {1} {m} \sum_{i=0}^n ( \theta_0 + \theta_1 ( x^{(i)} ) - y^{(i)} ) \cdot x$

Correctly Applying Gradient Descent

$ temp0 := \theta_0 - \alpha \frac {\partial} {\partial\theta_0} J(\theta_0,\theta_1) $

$ temp1 := \theta_1 - \alpha \frac {\partial} {\partial\theta_1} J(\theta_0,\theta_1) $

$ \theta_0 := temp0 $

$ \theta_1 := temp1 $

We are simultaneously updating $\theta_0$ and $\theta_1$. The reason why we store our new $\theta$ values in a temp variable is because we don’t want the newly updated value of $\theta_0$ to affect $\theta_1$. After both are assigned to temp variables we redefine them.

Example

Here is a simpler example to illustrate simultaneous updating.

$\text{ Let $ \theta_0 = 1 $, $ \theta_1 = 2 $, and $ \theta_j := \theta_j - \sqrt{\theta_0 \theta_1} $ }$

$ temp0 := 1 - \sqrt{1 \cdot 2} $

$ temp1 := 2 - \sqrt{1 \cdot 2} $

$ \theta_0 := temp0 = 1 - \sqrt{2} $

$ \theta_1 := temp1 = 2 - \sqrt{2} $

More Examples

In the following pictures we are going to assume that $ \theta_0 = 0 $ so that we end up with a 2-d graph instead of a 3-d representation. The concepts are still the same.

Learning Rate

The learning rate is a constant that determines how large of a jump our descent takes. A large learning rate causes a large jump in our $\theta$ values.

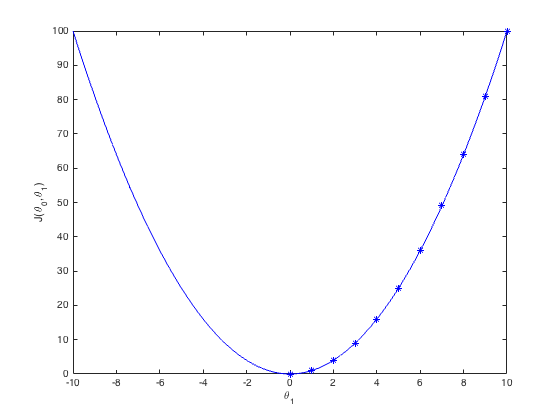
Each asterisk represents a step in the gradient descent. Above we stated that the learning rate determined the size of the step. The size of the step is directly correlated to the slop at that point. We see as the slope gets smaller the steps get smaller. Our $\alpha$ is being multiplied by a smaller slope causing a smaller step.

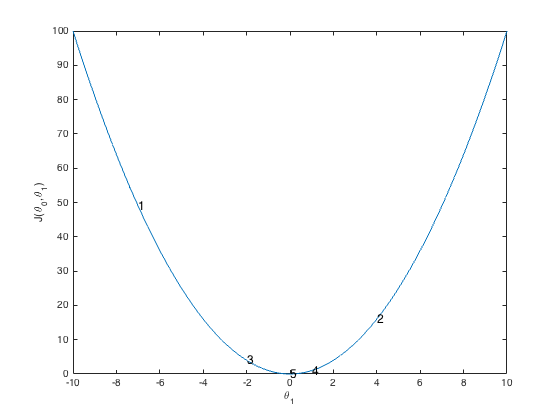
Here the jump is auto-corrected if it oversteps the minimum. At first glance it might not be clear why. On the right the slope is negative so the when multiplied by $\alpha$ it steps right. At number two the slope is positive which has an opposite sign as before causing it to step left. In this example the descent goes left and right of the minimum until it hits it.

Important Points

If we choose a learning rate that is too large, we will never converge on a point. This is because it constantly jumps to far left and right causing the slope to get larger and larger. The increasingly larger steps cause it to move further away from the minimum.

So what happens if we are already at the minimum with the values we chose. The algorithm is smart enough to stay where it is. Remember We are looking for a point where $ \theta_j := \theta_j - \alpha \frac {\partial} {\partial\theta_j} J(\theta_0,\theta_1) $. If we are at the minimum then the slope is zero meaning we don’t have to adjust our $\theta$ values.